La geometría es un área de la matemática que nos permite plasmar de diferentes maneras conceptos tan abstractos como el infinito o el concepto de medida, que nos parecen naturales, pero en realidad no lo son tanto. Al parecer todos nacemos con estos conceptos definidos, aunque nadie nos los haya explicado, de hecho, Euclides, el padre de la geometría, define a punto como “lo que no tiene parte”, y se dice que lo explicaba como lo que todos nos imaginamos cuando cerramos nuestros ojos. Esto puede parecer una anécdota, sin embargo, me parece que es una manifestación de la memoria del origen que todos traemos.
Una vez comprendido el concepto de punto, podemos tomar cantidades infinitas de ellos para formar líneas y figuras en un plano (que es infinito por supuesto), y es ahí donde aparece el círculo, esta figura que se define como el lugar geométrico de puntos del plano que equidistan de un punto llamado centro. Tal distancia la llamamos radio, y aunque el centro no es parte del círculo, sin él no lo podemos definir. Es algo así como un elemento indispensable, a la misma distancia de todos, que sabemos que existe y que conocemos, pero que no podemos tocar. A mi parecer, es como el gran sol central y nosotros en este plano físico.
Ya teniendo el círculo definido en el plano, podemos pasar a 3 dimensiones, y es ahí donde aparecen las curvas y superficies, que, por supuesto hay infinitas de ellas, pero siempre hay algunas más interesantes y estudiadas. Una es la espiral ascendente (en matemática le llamamos hélice). Lo interesante de esta curva, es que una definición de ella parametrizada respecto al parámetro real t es r(t)=(R cos(t), R sen(t), ct), donde las primeras 2 expresiones definen un círculo de radio R en el plano, y c marca la distancia entre un punto de la espiral y el siguiente en la misma posición del plano XY cuando dimos una vuelta completa.
Ahora bien, si miramos la espiral sólo en el plano, vemos un círculo, pero si ampliamos nuestra perspectiva y vemos más allá, nos damos cuenta de que hay una curva infinita hacia arriba y abajo, una hélice o espiral ascendente que nunca termina, al igual que los Números Reales, nuestra experiencia de vida, y el aprendizaje del amor.
Por otra parte, si hacemos girar un círculo respecto a uno de sus diámetros, entonces lo que obtendremos es una esfera. Nuevamente podemos confundirla con un círculo si la vemos en un plano, pero debemos estar atentos a los movimientos, definiciones y resultados, no dejarnos influenciar por las apariencias. No vemos al círculo girando, pero sabemos que necesita hacerlo para formar la esfera, que por supuesto corresponde a una colección infinita de puntos del especio, que equidistan de un punto llamado centro, el cual no es parte de la esfera, pero que sin él no se puede definir. Entonces, es una definición totalmente equivalente a la de círculo, pero en una nueva dimensión. ¿Cuántas dimensiones más hay donde podamos definir estos elementos? ¿En cuántas dimensiones más existimos?
Todo esto es en el mundo de la increíble Geometría Euclideana, donde se cumplen los 5 postulados de Euclides; aunque los matemáticos, como buenos científicos curiosos que deben(mos) ser, se pusieron a pensar en cómo sería una geometría que no cumpla uno de estos postulados, y “eligieron” el quinto que dice: Dada una recta y un punto exterior a ella, existe sólo una recta que pase por este punto y sea paralela a la recta dada (es la versión simplificada), y es ahí donde nacen las geometrías no euclideanas o absolutas.
Una de ellas, muy interesante y mi favorita, es la geometría hiperbólica, en particular el modelo del Disco de Poincaré, donde se ejemplifican conceptos de infinitud de manera excepcional. La geometría hiperbólica del disco de Poincaré se define en un disco, es decir, un círculo lleno. En este disco definiremos las rectas como las líneas que pasan por el centro, como lo que dibujamos para medir el diámetro, pero también llamaremos rectas a círculos perpendiculares al borde, ¡y es aquí donde comienza la magia! Hasta ahora siempre supimos que las rectas las podemos dibujar con regla, eso en la geometría euclideana, pero si cambiamos las definiciones iniciales, entonces las rectas ya no son siempre “rectas”, y pueden ser curvas al verlas con los ojos Euclideanos. Así que nos pondremos los lentes de la geometría hiperbólica y comprenderemos que, como todo en matemática, los elementos se definen, y así mismo hicimos con las rectas.
Veamos un ejemplo gráfico donde vemos los 2 tipos de rectas que podemos encontrar.
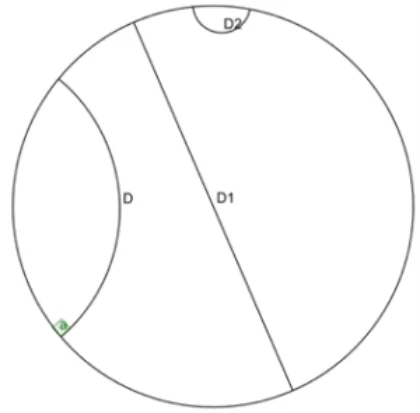
Es fácil convencerse de que, si trazamos una recta y un punto externo a ella, podemos encontrar más de una recta que pase por el punto (de hecho, infinitas) y que no toque a la primera recta dada, lo cual contradice el quinto postulado de Euclides, que es lo que esperábamos por ser una geometría absoluta.
Ya sabiendo esto, podemos profundizar mucho más e incluso hacer polígonos en ella, con interesantes características matemáticas, como aplicar acciones de grupos, analizar sus representaciones simplécticas, etc., pero también comenzamos a detectar esta geometría en otras áreas del conocimiento, y es así como nos podemos maravillar con algunas obras de arte de Maurits Cornelis Escher, un artista neerlandés nacido en 1972, conocido por sus teselaciones y figuras “imposibles” y mundos “imaginarios” (pongo comillas pues me cuestiono, que tanto de su obra puede ser inspiración superior o recuerdos de la verdadera vida?)
Escher entre sus tantas obras, dedica un espacio especial a las teselaciones o embaldosados en el disco de Poincaré. Para muchos es una linda obra de arte, pero los curiosos matemáticos comprobaron la exactitud de sus dibujos y concluyeron que sus cálculos son perfectos. Y entonces nos preguntamos, ¿qué tanta matemática sabía Escher? Efectivamente él estudió parte de la carrera de arquitectura, donde se enseñan conceptos de matemática, sin embargo, la geometría hiperbólica generalmente se estudia en profundidad en estudios de postgrado de ciencias matemáticas. ¿Habrá hecho los cálculos? Yo lo dudo, creo que es una manifestación de la perfección superior en un dibujo, arte verdadero.
Fresia Castro nos dice que el Método Cyclopea es una esfera infinita hacia adentro y hacia fuera, y seguramente todos los pinealistas tenemos una percepción de ese concepto. En mi caso, puedo percibir que las obras de Escher lo plasman maravillosamente.

Si observamos la imagen de la izquierda, podemos ver que hay muchos triángulos hiperbólicos, y mientras más lejos del centro, más pequeños se ven, eso es pues los estamos viendo con los “ojos euclideanos”, pero si lo vemos con los “ojos hiperbólicos”, todos son del mismo tamaño. Lo que pasa es que tal como se definieron de una manera distinta las rectas, la medida también es diferente aquí (no entraremos en detalles, pero se hace con la función logaritmo).
Tenemos entonces una figura con infinitos triángulos, que mientras más se acercan al borde, más pequeños los vemos, y sin embargo, son infinitos, pero a la vez forman una figura acotada en este plano, tal como es el Método Cyclopea.
En esta otra imagen podemos observar como la definición es al revés, las figuras esta vez las vemos más pequeñas hacia el centro y más grandes hacia el borde. Nunca terminan, nunca tocan el centro, convergen al punto central, como el centro del círculo, aunque sólo lo tocan tendiendo al infinito.
Aquí me detengo a pensar en la relación con nosotros, no podemos tocar el borde ni el centro, tal como nosotros al plano electrónico, aunque lo sentimos, lo experienciamos, conectamos con él, pero la única forma de tocarlo es “tendiendo al infinito”, convergiendo al él, es decir, ascensionando.




